KEY TAKEAWAYS
- Selling puts is not more risky than investing in the underlying security. It can even be argued that it is less risky
- There is no difference in the payoff profile between selling a put and a covered call position in the same underlying security
Brief Update on Options
This article is not meant to be a detailed guide on all aspects of options and trading in options. If you want a more detailed overview of options, please see the lessons in our options course ranging from basic concepts of options to more advanced pricing concepts.
An option is a contract giving the buyer the right, but not the obligation, to buy (in the case of a call) or sell (in the case of a put) the underlying asset at a specific price on or before a certain date. Conversely a contract obligates the seller to sell (in the case of a call) or buy (in the case of a put) the underlying asset at a specific price on or before a certain date if the buyer decides to exercise his right.
The option buyer pays an upfront premium to the seller for the right to put or call the underlying security at the agreed upon price (the strike price).
The buyer is also said to be long the option and the seller is said to be short having sold (or written) the option to the buyer.
Below we have included simple illustrations showing the payoff profiles of long and short positions in a call or put option on a stock (could be any security) as a function at the underlying stock price on thee exercise date with the strike price denoted as S.
Simply stated as the buyer of the option pays a premium to the seller upfront the breakeven profitability point between buyer and seller is when the stock price at expiry exceed the strike price by the amount of the premium (in the case of a call) or when the stock price at expiry falls below the stock price by the amount of the premium (in the case of a put).
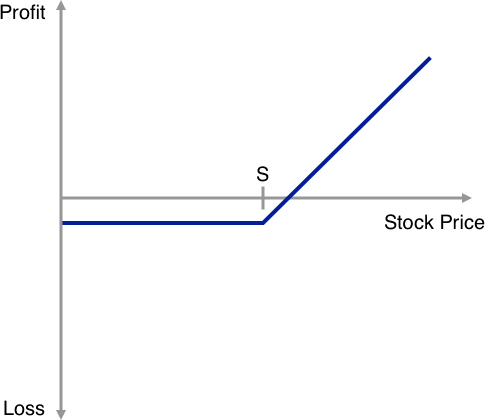
Long Call 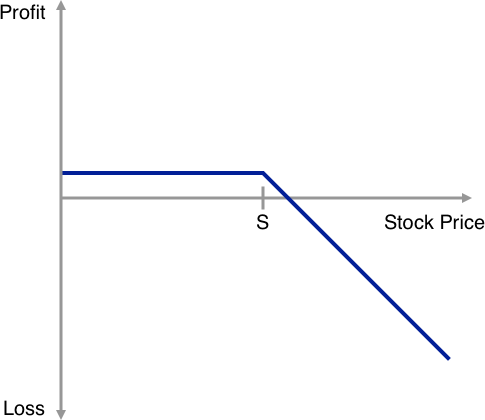
Short Call 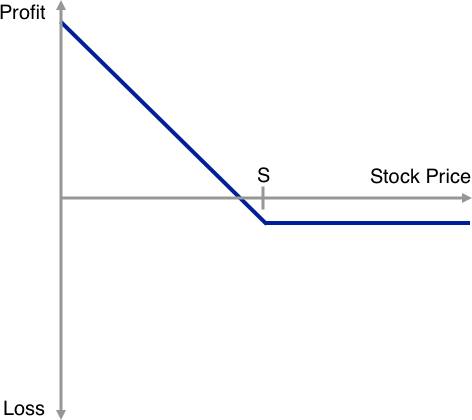
Long Put 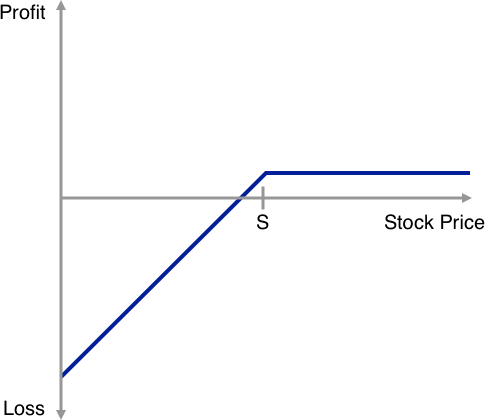
Short Put
Risk Profile of Selling / Writing Puts
Below we have illustrated the payoff profile a short put option compared to holding a long position in the underlying stock. If we define risk as the chance of making a loss it is easy to derive from the two illustrations that selling a put is no more risky than holding a long position in the underlying stock. In fact, we can even conclude that selling a put is less risky as the premium received upfront from the buyer of the put moves the breakeven point of the short put further to the left vs. the long position in the underlying stock.

Short Put 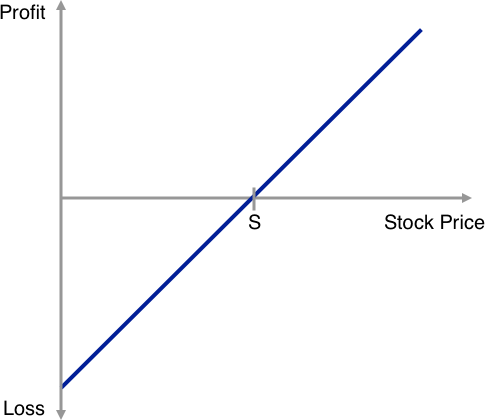
Long Stock Position
Covered Call vs. Short Put
A covered call call writer already owns the equivalent amount of the underlying security in their portfolio (or alternatively buys the underlying security at the same time as writing the call). To execute a covered call, an investor holding a long position in an asset then sells call options on that same asset to generate an income stream. The investor’s long position in the asset is the “cover” because it means the seller can deliver the shares if the buyer of the call option chooses to exercise.
There is a general misconception that selling puts is somehow more risky than a covered call. But let’s explore the payoff profile of the covered call a bit further by combining the payoff profiles above of a long stock position and a short call position in the same stock.
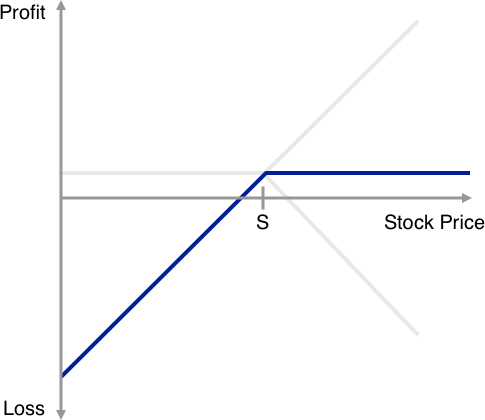
Effectively, above the strike price the long stock position and the short call cancel each other out (or in other words the long stock position covers the loss from the the short call) resulting the payoff profile illustrated by the blue line.
As you can see this payoff profile is exactly the same as the payoff profile of the short put from above. In other words, a short put position and a covered call position have equivalent payoff profiles.
Put-Call Parity Approach
Another way we can illustrate the point of a short put and a covered call having the same payoff profile, is by using the put-call parity.
The put-call parity states that simultaneously holding a short European put and long European call of the same class will deliver the same return as holding one forward contract on the same underlying asset, with the same expiration, and a forward price equal to the option’s strike price. If the prices of the put and call options diverge so that this relationship does not hold, an arbitrage opportunity exists, meaning that sophisticated traders can theoretically earn a risk-free profit. Such opportunities are uncommon and short-lived in liquid markets.
The equation expressing put-call parity is:
C + PV(S) = P + K
where:
C = price of the European call option
PV(S) = the present value of the strike price (S), discounted from the value on the expiration date at the risk-free rate
P = price of the European put
K = spot price or the current market value of the underlying asset
So by rearranging the put-call parity formula we can define a short put as:
-P = K – C – PV(S)
At expiry the present value of the strike price is of course the strike price itself so:
-P = – C + (K – S)
So the short put payoff is equivalent to that of a short call plus the difference between the price of the underlying and the strike price which again is exactly the payoff from a covered call position.






0 Comments